1. 基础
1.1 神经网络基本工作原理
1.1.1 神经元的数学模型

input 输入
训练样本,一般训练样本是多个属性,如果要预测房价,所以$x_1$可能代表面积,$x_2$可能代表地理位置,$x_3$代表朝向。
weights 权重
$w_1$是输入信号的权重值,衡量当前输入的比重。
bias 偏移
在生物学中,当脑神经细胞电平大于某个临界值时,神经元细胞才会处于兴奋状态,这个b就是实际那个临界值。
当$w_1x_1 + w_2x_2 + w_3*x_3>=t$时,该神经元才会兴奋,把t移动到左边来,他就是b。
激活函数
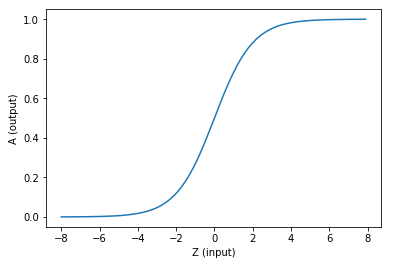
求和之后,神经细胞已经处于兴奋状态,已经决定向下一个神经元传递信号了,但是要传递更多强烈的信号,需要激活函数来确定:
$$A=\sigma(Z)$$
生物钟信号是一个渐变的过程,所以是个曲线。
1.1.2 神经网路的训练过程
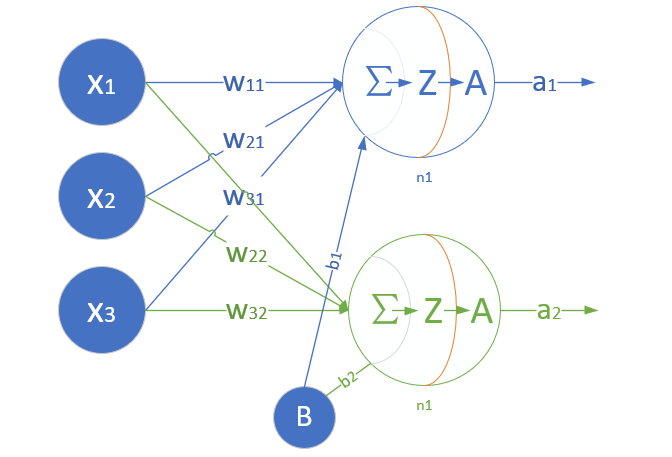
这是一个单层的神经网络,有 m 个输入 (这里 m=3),有 n 个输出 (这里 n=2)。在神经网络中,b 到每个神经元的权值来表示实际的偏移值,亦即 (b1,b2),这样便于矩阵运算。也有些人把 b 写成 x0,其实是同一个效果,即把偏移值看做是神经元的一个输入。
- (x1,x2,x3) 是一个样本数据的三个特征值
- (w11,w21,w31) 是 (x1,x2,x3) 到 n1 的权重
- (w12,w22,w32) 是 (x1,x2,x3) 到 n2 的权重
- b1 是 n1 的偏移
- b2 是 n2 的偏移
同一个特征 x1,对于n1,n2来说,权重是不相同的,因为 n1,n2 是两个神经元,它们完成不同的任务(特征识别)。我们假设 x1,x2,x3 分别代表红绿蓝三种颜色,而 n1,n2 分别用于识别暖色和冷色,那么 x1 到 n1 的权重,肯定要大于 x1 到 n2 的权重,因为 x1 代表红色,是暖色。
而对于 n1 来说,x1,x2,x3 输入的权重也是不相同的,因为它要对不同特征有选择地接纳。如同上面的例子,n1 对于代表红色的 x1,肯定是特别重视,权重值较高;而对于代表蓝色的 x3,尽量把权重值降低,才能有正确的输出。
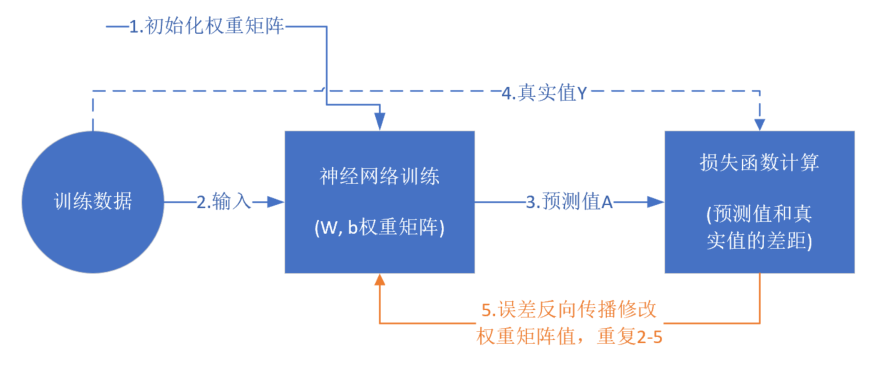
训练流程
1.1.3 神经网络中的矩阵运算

$$
z1_1 = x_1 \cdot w1_{1,1}+ x_2 \cdot w1_{2,1}+b1_1
$$
$$
z1_2 = x_1 \cdot w1_{1,2}+ x_2 \cdot w1_{2,2}+b1_2
$$
$$
z1_3 = x_1 \cdot w1_{1,3}+ x_2 \cdot w1_{2,3}+b1_3
$$
变成矩阵运算:
$$
z1_1=
\begin{pmatrix}
x_1 & x_2
\end{pmatrix}
\begin{pmatrix}
w1_{1,1} \\
w1_{2,1}
\end{pmatrix}
+b1_1
$$
$$
z1_2=
\begin{pmatrix}
x_1 & x_2
\end{pmatrix}
\begin{pmatrix}
w1_{1,2} \\
w1_{2,2}
\end{pmatrix}
+b1_2
$$
$$
z1_3=
\begin{pmatrix}
x_1 & x_2
\end{pmatrix}
\begin{pmatrix}
w1_{1,3} \\
w1_{2,3}
\end{pmatrix}
+b1_3
$$
再变成大矩阵:
$$
Z1 =
\begin{pmatrix}
x_1 & x_2
\end{pmatrix}
\begin{pmatrix}
w1_{1,1}&w1_{1,2}&w1_{1,3} \\
w1_{2,1}&w1_{2,2}&w1_{2,3} \\
\end{pmatrix}
+\begin{pmatrix}
b1_1 & b1_2 & b1_3
\end{pmatrix}
$$
最后变成矩阵符号:
$$Z1 = X \cdot W1 + B1$$
然后是激活函数运算:
$$A1=a(Z1)$$
同理可得:
$$Z2 = A1 \cdot W2 + B2$$
注意:损失函数不是前向计算的一部分。
1.1.4 神经网络的主要功能
回归(regression)或者拟合(Fitting)
单层神经网络模拟一条直线,完成线性分割。两层神经网络可以无限逼近任意函数。
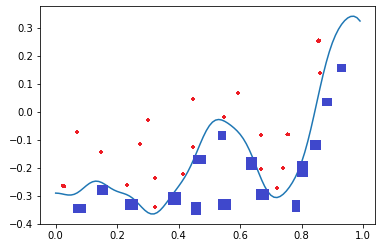
图1-18所示就是一个两层神经网络拟合复杂曲线的实例。
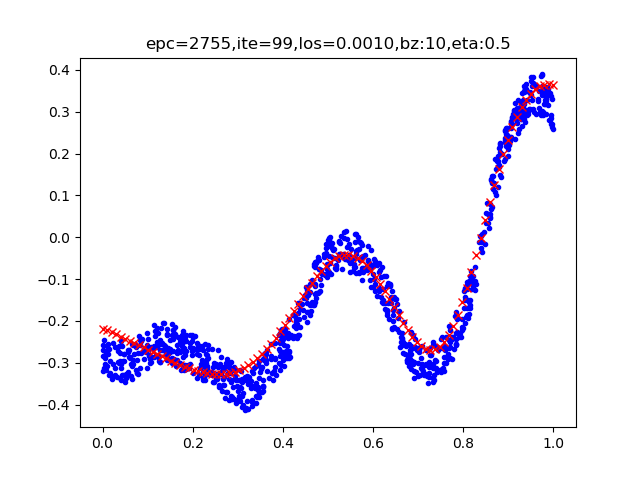
图1-18 回归/拟合示意图
所谓回归或者拟合,其实就是给出x值输出y值的过程,并且让y值与样本数据形成的曲线的距离尽量小,可以理解为是对样本数据的一种骨架式的抽象。
分类(Classification)
区分图片中红色和蓝色的点的边界,分类就是对两类或多类样本数据的边界的抽象。
这么复杂的函数,需要两层以上的神经网络。从输入层到隐藏层的矩阵计算,就是对输入数据进行了空间变换,让它可以线性可分,然后在输出上画出一个分界线。而训练的过程,就是那个空间变换的过程。



